-
[TIL]자료구조 - 이진트리알고리즘 2024. 10. 20. 13:52
이진트리
이진트리는 각 노드가 최대 2개의 자식을 가질 수 있는 트리 를 의미한다
이진트리의 탐색
이진트리의 탐색은 재귀를 이용하여 비교적 쉽게 구현할 수 있다.
방문하는 순서에따라 이진트리 탐색은 3가지로 나뉘게되는데 전위 탐색, 중위 탐색, 후위 탐색이다.
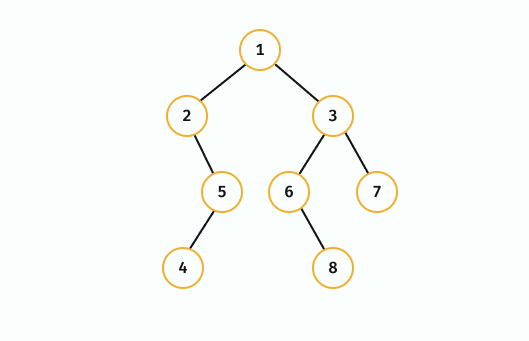
이진트리 예제 전위탐색(preorder)
<부모 - 왼쪽 - 오른쪽> 순서로 탐색하는 방식
위 예제를 탐색한다면 <1-2-5-4-3-6-8-7> 순서로 방문하게된다.
중위탐색(inorder)
<왼쪽 - 부모 - 오른쪽> 순서로 탐색하는 방식
위 예제를 탐색한다면 <2-4-5-1-6-8-3-7> 순서로 방문하게된다.
후위탐색(postorder)
<왼쪽 - 오른쪽 - 부모> 순서로 탐색하는 방식
위 예제를 탐색한다면 <4-5-2-8-6-7-3-1> 순서로 방문하게된다.
이진탐색트리
이진트리의 조건중 하나를 추가한 것.
"부모의 왼쪽 방향에 있는 노드들은 전부 부모 보다 값이 작아야 하고, 부모의 우측 방향에 있는 노드들은 전부 부모 보다 값이 커야만 한다"는 조건
완전이진트리
트리의 모든 값이 왼쪽에서 순서대로 차 있는 것. 완전 이진 트리를 배열에 채우게 되면, 중간에 비는 값 없이 일자로 채워진다.

완전이진트리 예시 
완전이진트리를 배열로 표현하기 (빈칸x) max-heap
모든 노드에 대해 부모 노드가 자신의 자식 노드가 갖는 값보다 같거나 크다면 이는 Max-Heap이다. Max Heap의 가장 중요한 특징 중 하나는, 루트 노드에는 항상 최댓값이 항상 들어 있다
이렇게 max-heap을 만드는 데는 시간이 만큼 소요되지만, 그 이후 특정 원소 하나를 삭제, 삽입했을 때에는 완전 이진 트리에서의 삽입 삭제이므로 시간만 소요가 됩니다. 최댓값은 루트 노드이므로 max-heap이 만들어져 있는 상황이라면 의 시간이 소요된다. min-heap 구조도 max-heap 구조와 정확히 동일하다
다만, max-heap에서의 삭제는 루트 노드에서만 가능합니다. max-heap을 이용하면 삽입, 삭제에 만큼의 시간만 소요하여 그 다음 최댓값을 루트로 올려줄 수 있지만 삭제는 항상 루트 노드만 가능함에 꼭 유의합니다. 또한 max-heap에서는 k 번째 최댓값을 구할 수 없습니다. 항상 가장 큰 값이 무엇인지만 알 수 있는 자료구조입니다. 따라서 루트 노드를 제외하고는 다른 원소들이 어느 위치에 있을지 아무도 알 수 없습니다. 끝으로 n개의 숫자들 중 최댓값을 단 한 번만 찾아야 하는 경우라면 max-heap을 만든 뒤 루트 노드를 봐야하므로 시간이 만큼 소요되기 때문에, 이 경우에는 간단히 순차탐색을 통해 에 최댓값을 찾는 것이 더 편리합니다. 이처럼 원소의 추가, 그리고 최댓값의 삭제가 빈번하게 일어나는 상황에서 현재 남아있는 원소들 중 최댓값을 빠르게 계속 얻고 싶은 경우에만 heap 자료구조가 유용하다는 사실을 꼭 이해하고 넘어가야 합니다.
'알고리즘' 카테고리의 다른 글
[알고리즘] 재귀함수 활용해보기 (0) 2024.11.27 [알고리즘] java 좌표정렬 (compareTo) (0) 2024.11.17 [알고리즘] 삽입정렬 (0) 2024.11.14 [알고리즘] 버블정렬 (0) 2024.11.13 [알고리즘] 선택정렬 (0) 2024.11.13